Bạn đang xem bài viết Cách tính diện tích tứ giác và ví dụ về áp dụng công thức tại Neu-edutop.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Diện tích tứ giác là một khái niệm quan trọng trong toán học, đặc biệt trong hình học. Việc tính toán diện tích tứ giác có thể áp dụng vào nhiều lĩnh vực, như kiến trúc, xây dựng, địa lý và cả trong cuộc sống hàng ngày. Để tính diện tích của một tứ giác, chúng ta có nhiều phương pháp khác nhau, tuy nhiên trong bài viết này, chúng ta sẽ tập trung vào công thức tính diện tích tứ giác và cách áp dụng nó để giải quyết bài toán.
Ví dụ về áp dụng công thức là: Cho tứ giác ABCD có độ dài các cạnh lần lượt là AB = 5 cm, BC = 8 cm, CD = 6 cm và DA = 7 cm. Tìm diện tích của tứ giác ABCD.
Mục lục nội dung
Cách tính diện tích tứ giác, phương thức tính diện tích tứ giác là một trong những kiến thức cần biết khi học hình học phẳng. Với bài viết này, Neu-edutop.edu.vn sẽ hướng dẫn các bạn cách tính diện tích tứ giác kèm thêm các ví dụ minh họa cách tính.

1. Công thức tính diện tích tứ giác
1.1. Công thức tính diện tích hình vuông

Công thức tính diện tích hình vuông là: (S = a.a)
Trong đó:
– S là diện tích hình vuông.
– a là chiều dài cạnh hình vuông.
1.2. Công thức tính diện tích hình chữ nhật
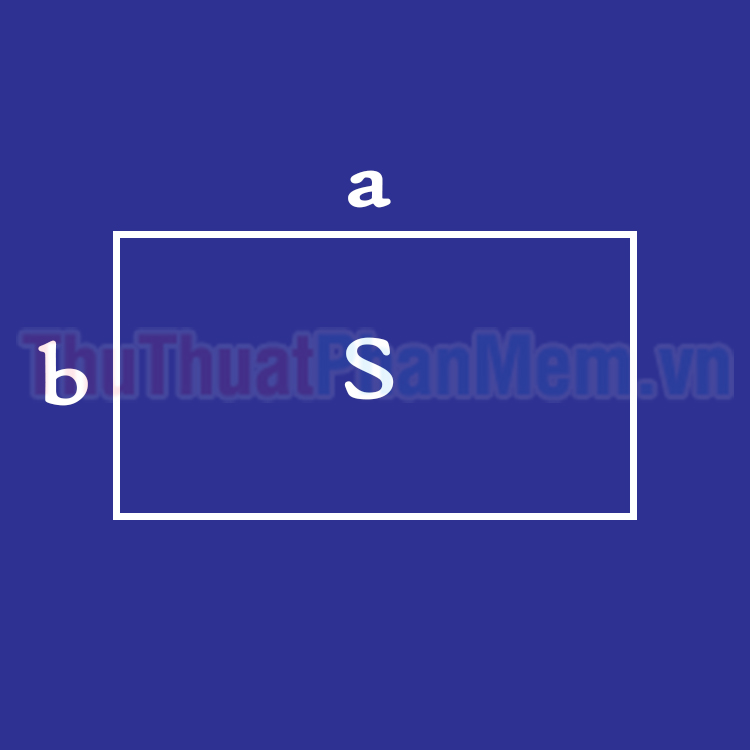
Công thức tính diện tích hình chữ nhật là: (S = a.b)
Trong đó:
– S là diện tích hình chữ nhật.
– a là chiều dài hình chữ nhật.
– b là chiều rộng hình chữ nhật.
1.3. Công thức tính diện tích hình thang
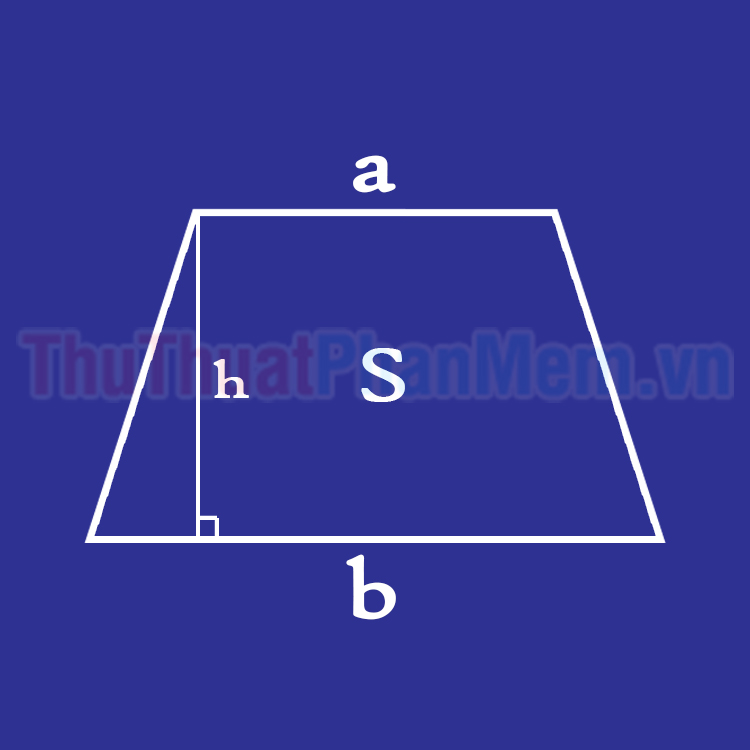
Công thức tính diện tích hình thang là: (S = (a + b).h.frac{1}{2})
Trong đó:
– S là diện tích hình thang.
– a và b là hai cạnh đáy của hình thang.
– h là chiều cao khoảng cách giữa hai đáy hình thang.
1.4. Công thức tính diện tích hình bình hành
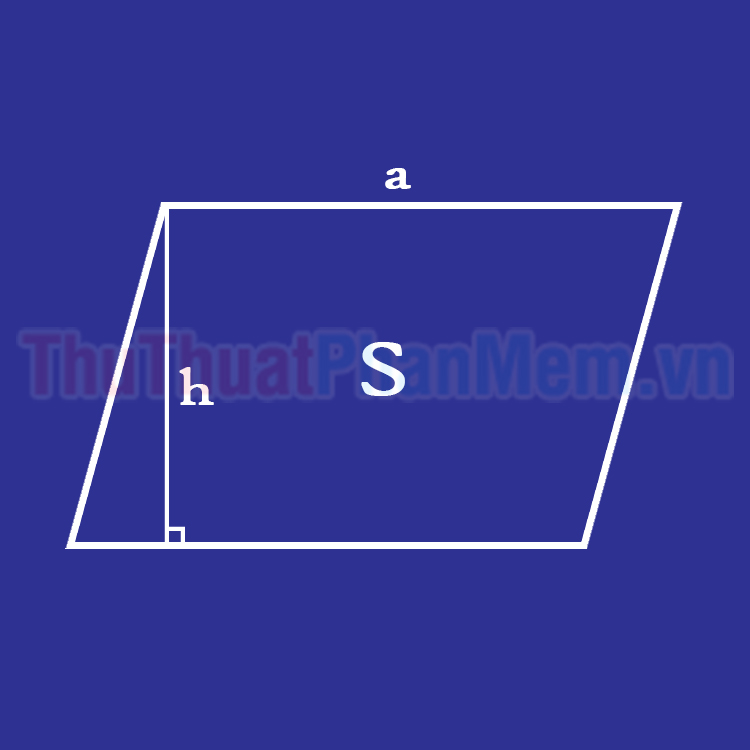
Công thức tính diện tích hình bình hành là: (S = a.h)
Trong đó:
– S là diện tích hình bình hành.
– a là cạnh đáy của hình bình hành.
– h là chiều cao khoảng cách giữa hai đáy của hình bình hành.
1.5. Công thức tính diện tích hình thoi
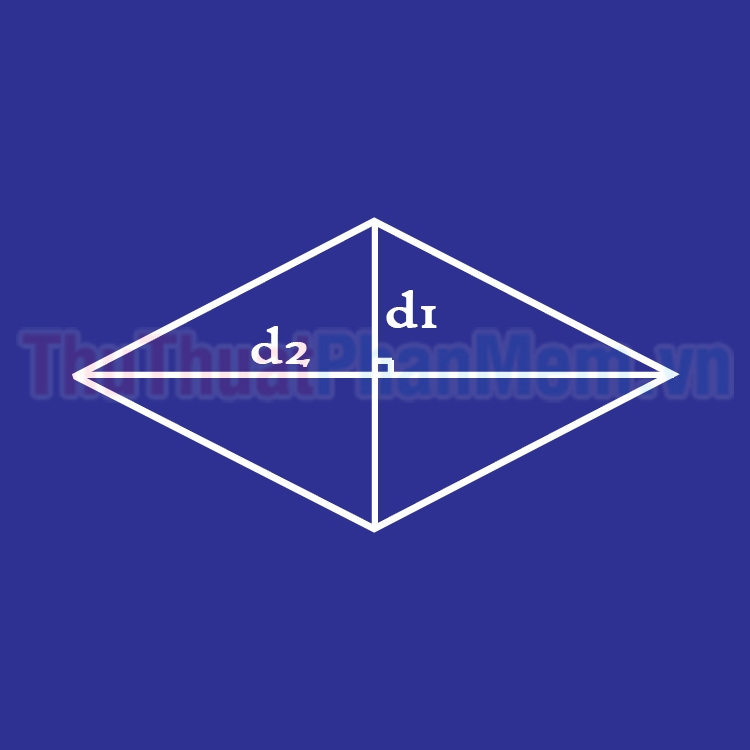
Công thức tính diện tích hình thoi là: (S = d1.d2.frac{1}{2})
Trong đó:
– S là diện tích hình thoi.
– d1 và d2 là hai đường chéo của hình thoi.
2. Ví dụ minh họa tính diện tích tứ giác
Ví dụ 1: Tính diện tích hình vuông có cạnh là 5 cm.
Diện tích hình vuông có cạnh dài 5 cm là: (S = a.a = 5.5 = 25(c{m^2}))
Vậy diện tích hình vuông đó là (25c{m^2}).
Ví dụ 2: Tính diện tích hình chữ nhật có chiều dài là 6 cm và chiều rộng là 4 cm.
Diện tích hình chữ nhật có cạnh dài là 6 cm và cạnh rộng là 4 cm là: (S = a.b = 6.4 = 24(c{m^2}))
Vậy diện tích hình chữ nhật đó là (24c{m^2}).
Ví dụ 3: Tính diện tích hình thang có chiều dài đáy rộng là 4 cm và chiều dài đáy hẹp là 3 cm cùng với chiều cao là 2 cm.
Diện tích hình thang có chiều dài hai đáy lần lượt là 4 cm và 3 cm cùng chiều cao 2 cm là: (S = (a = b).h.frac{1}{2} = (4 + 3).2.frac{1}{2} = 7(c{m^2}))
Vậy diện tích của hình thang đó là (7c{m^2}).
Ví dụ 4: Tính diện tích hình bình hành có cạnh đáy dài 5 cm và chiều cao dài 3 cm.
Diện tích hình bình hành có cạnh đáy dài 5 cm và chiều cao dài 3 cm là: (S = a.h = 5.3 = 15(c{m^2}))
Vậy diện tích của hình bình hành đó là (15c{m^2}).
Ví dụ 5: Tính diện tích hình thoi có hai đường chéo lần lượt là 4 cm và 6 cm.
Diện tích hình thoi có hai đường chéo là 4 cm và 6 cm là: (S = d1.d2.frac{1}{2} = 4.6.frac{1}{2} = 12(c{m^2}))
Cảm ơn các bạn đã đọc bài viết của Neu-edutop.edu.vn.vn chúng tôi về cách tính diện tích các tứ giác cùng các ví dụ minh họa đi kèm. Chúc các bạn thành công.
Tổng hợp các cách tính diện tích tứ giác như sử dụng công thức Heron, Phân kỳ, và phương pháp tính diện tích bằng cách tách tứ giác thành hai tam giác, tất cả các phương pháp này đều đem lại kết quả chính xác cho diện tích tứ giác. Thông qua đó, chúng ta có thể ứng dụng công thức để giải quyết những bài toán liên quan đến diện tích tứ giác, như bài toán tìm diện tích hình thoi, hình bình hành, hay tìm diện tích một bề mặt tam giác trong không gian. Việc hiểu và nắm vững các cách tính này sẽ giúp cho các bạn học sinh, sinh viên có thể xử lý tốt hơn các bài tập, bài toán liên quan đến diện tích tứ giác.
Cảm ơn bạn đã xem bài viết Cách tính diện tích tứ giác và ví dụ về áp dụng công thức tại Neu-edutop.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Nguồn: https://thuthuatphanmem.vn/cong-thuc-tinh-dien-tich-tu-giac-va-vi-du-minh-hoa/
Từ Khoá Tìm Kiếm Liên Quan:
1. Diện tích tứ giác
2. Công thức tính diện tích tứ giác
3. Tứ giác lồi và có góc tù
4. Tứ giác nội tiếp và ngoại tiếp
5. Ví dụ tính diện tích tứ giác ABCD
6. Tính diện tích tứ giác khi biết cạnh, đường cao, đường trung tuyến
7. Sử dụng định lí Heron để tính diện tích tứ giác
8. Tạo hình tứ giác và tính diện tích bằng phần mềm Geogebra
9. Các bước giải bài tập tính diện tích tứ giác
10. Ứng dụng tính diện tích tứ giác trong giải toán hình học.